Generate Random Points over the Disk
Kevin Liu
5/24/2020
To generate random points over the disk with radius \(=r\)
1. Generate \(U_1 \sim\) uniform(0,1) and \(U_2 \sim\) uniform(0,1), independent.
2. Set \(X = r \sqrt{U_2} \cos(2\pi U_1)\) and \(Y = r \sqrt{U_2} \sin(2\pi U_1)\)
Proof:
\[ \begin{cases} X=r \sqrt{U_{2}} \cos \left(2 \pi U_{1}\right)\\ Y=r \sqrt{U_{2}} \sin \left(2 \pi U_{1}\right) \end{cases} \Longrightarrow \begin{cases} U_1 = \frac{1}{2\pi}\arctan\frac{Y}{X}\\ U_2 = \frac{X^2+Y^2}{r^2} \end{cases} \]
\[ \mathcal{J} = \begin{bmatrix} \frac{\partial U_1}{\partial X} & \frac{\partial U_1}{\partial Y}\\ \frac{\partial U_2}{\partial X} & \frac{\partial U_2}{\partial Y} \end{bmatrix} = \begin{bmatrix} \frac{-Y}{2\pi(X^2+Y^2)} & \frac{X}{2\pi(X^2+Y^2)}\\ \frac{2X}{r^2} & \frac{2Y}{r^2} \end{bmatrix} \Longrightarrow \det(\mathcal{J}) = \frac{1}{\pi r^2} \]
\[ f_{X,Y}(x,y) = f_{U_1,U_2}(\frac{1}{2 \pi} \arctan \frac{Y}{X}, \frac{X^{2}+Y^{2}}{r^{2}}) \det(\mathcal{J}) = \frac{1}{\pi r^2} \]
Hence, be definition, \(f_{X,Y}(x,y)\) is uniformly distributed in the disk with radius \(=r\).
A common mistake is using \(\begin{cases} X=r U_{2} \cos \left(2 \pi U_{1}\right)\\ Y=r U_{2} \sin \left(2 \pi U_{1}\right) \end{cases}\) instead of \(\begin{cases} X=r \sqrt{U_{2}} \cos \left(2 \pi U_{1}\right)\\ Y=r \sqrt{U_{2}} \sin \left(2 \pi U_{1}\right) \end{cases}\).
Code in python to generate random points over the unit disk:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(524)
U1 = np.random.uniform(size = 10000)
U2 = np.random.uniform(size = 10000)
r = 1
X = r * np.sqrt(U2) * np.cos(2 * np.pi * U1)
Y = r * np.sqrt(U2) * np.sin(2 * np.pi * U1)
circle = plt.Circle((0, 0), 1, color='g', fill=False)
fig,ax = plt.subplots()
ax.scatter(x = X, y = Y, s = 0.3)
ax.add_artist(circle)
plt.show()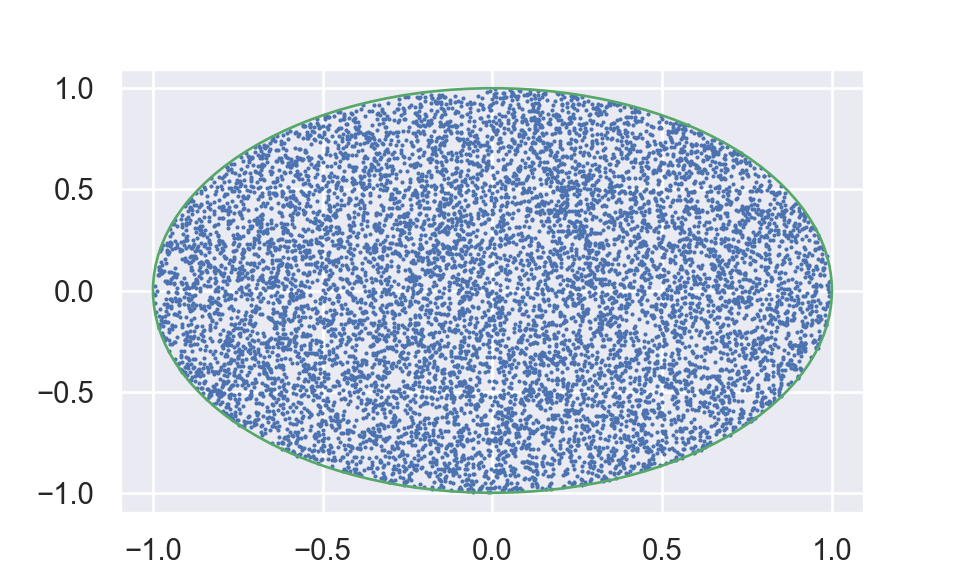
plt.close()